import pandas as np
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
from datetime import timedelta
import pandas as pdMultivariate GARCH in Tensorflow/Keras
Not investment advice - use at your own risk.
Conditional volatility and correlation using multivariate GARCH on DAX and S&P500. Implementation with Tensorflow/Keras.
Still under development - corresponding blogpost coming soon.
import yfinance as yf
data = yf.download("^GDAXI ^GSPC", start="2017-09-10", end="2022-09-10", interval="1d")
close = data["Close"]
returns = np.log(close).diff().dropna()
fig, axs = plt.subplots(2,1, figsize = (22,5*2))
for i in range(2):
axs[i].plot(returns.iloc[:,i])
axs[i].grid(alpha=0.5)
axs[i].margins(x=0)
axs[i].set_title("{} - log-returns".format(returns.columns[i]),size=20)[*********************100%***********************] 2 of 2 completed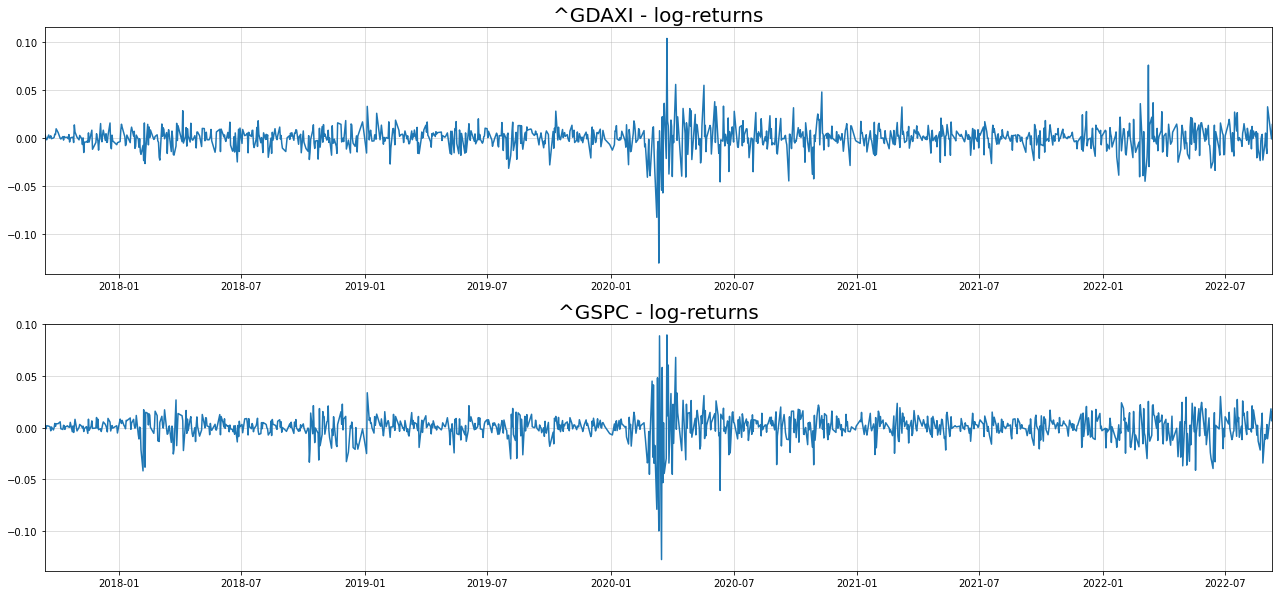
rolling_corrs = returns.rolling(60,min_periods=0).corr()
gdaxi_sp500_rollcorr = rolling_corrs["^GDAXI"][rolling_corrs.index.get_level_values(1)=="^GSPC"]
plt.figure(figsize = (22,5))
plt.title("60 day rolling correlation - DAX vs. S&P500",size=20)
plt.plot(returns.index[30:],gdaxi_sp500_rollcorr.values[30:],c="green", label="60 day rolling correlation")
plt.grid(alpha=0.5)
plt.margins(x=0)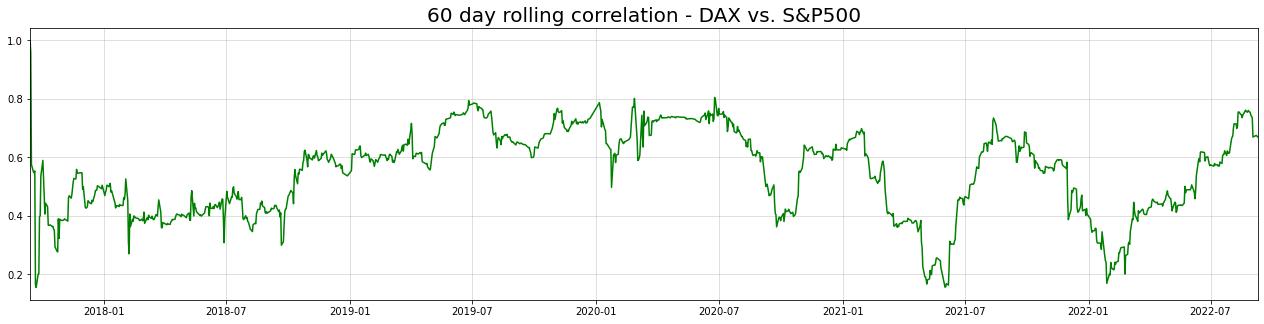
class MGARCH_DCC(tf.keras.Model):
"""
Tensorflow/Keras implementation of multivariate GARCH under dynamic conditional correlation (DCC) specification.
Further reading:
- Engle, Robert. "Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models."
- Bollerslev, Tim. "Modeling the Coherence in Short-Run Nominal Exchange Rates: A Multi-variate Generalized ARCH Model."
- Lütkepohl, Helmut. "New introduction to multiple time series analysis."
"""
def __init__(self, y):
"""
Args:
y: NxM numpy.array of N observations of M correlated time-series
"""
super().__init__()
n_dims = y.shape[1]
self.n_dims = n_dims
self.MU = tf.Variable(np.mean(y,0)) #use a mean variable
self.sigma0 = tf.Variable(np.std(y,0)) #initial standard deviations at t=0
#we initialize all restricted parameters to lie inside the desired range
#by keeping the learning rate low, this should result in admissible results
#for more complex models, this might not suffice
self.alpha0 = tf.Variable(np.std(y,0))
self.alpha = tf.Variable(tf.zeros(shape=(n_dims,))+0.25)
self.beta = tf.Variable(tf.zeros(shape=(n_dims,))+0.25)
self.L0 = tf.Variable(np.float32(np.linalg.cholesky(np.corrcoef(y.T)))) #decomposition of A_0
self.A = tf.Variable(tf.zeros(shape=(1,))+0.9)
self.B = tf.Variable(tf.zeros(shape=(1,))+0.05)
def call(self, y):
"""
Args:
y: NxM numpy.array of N observations of M correlated time-series
"""
return self.get_conditional_dists(y)
def get_log_probs(self, y):
"""
Calculate log probabilities for a given matrix of time-series observations
Args:
y: NxM numpy.array of N observations of M correlated time-series
"""
return self.get_conditional_dists(y).log_prob(y)
@tf.function
def get_conditional_dists(self, y):
"""
Calculate conditional distributions for given observations
Args:
y: NxM numpy.array of N observations of M correlated time-series
"""
T = tf.shape(y)[0]
#create containers for looping
mus = tf.TensorArray(tf.float32, size = T) #observation mean container
Sigmas = tf.TensorArray(tf.float32, size = T) #observation covariance container
sigmas = tf.TensorArray(tf.float32, size = T+1)
us = tf.TensorArray(tf.float32, size = T+1)
Qs = tf.TensorArray(tf.float32, size = T+1)
#initialize respective values for t=0
sigmas = sigmas.write(0, self.sigma0)
A0 = tf.transpose(self.L0)@self.L0
Qs = Qs.write(0, A0) #set initial unnormalized correlation equal to mean matrix
us = us.write(0, tf.zeros(shape=(self.n_dims,))) #initial observations equal to zero
#convenience
sigma0 = self.sigma0
alpha0 = self.alpha0**2 #ensure positivity
alpha = self.alpha
beta = self.beta
A = self.A
B = self.B
for t in tf.range(T):
#tm1 = 't minus 1'
#suppress conditioning on past in notation
#1) calculate conditional standard deviations
u_tm1 = us.read(t)
sigma_tm1 = sigmas.read(t)
sigma_t = (alpha0 + alpha*sigma_tm1**2 + beta*u_tm1**2)**0.5
#2) calculate conditional correlations
u_tm1_standardized = u_tm1/sigma_tm1
Psi_tilde_tm1 = tf.reshape(u_tm1_standardized, (self.n_dims,1))@tf.reshape(u_tm1_standardized, (1,self.n_dims))
Q_tm1 = Qs.read(t)
Q_t = A0 + A*(Q_tm1 - A0) + B*(Psi_tilde_tm1 - A0)
R_t = self.cov_to_corr(Q_t)
#3) calculate conditional covariance
D_t = tf.linalg.LinearOperatorDiag(sigma_t)
Sigma_t = D_t@R_t@D_t
#4) store values for next iteration
sigmas = sigmas.write(t+1, sigma_t)
us = us.write(t+1, y[t,:]-self.MU) #we want to model the zero-mean disturbances
Qs = Qs.write(t+1, Q_t)
mus = mus.write(t, self.MU)
Sigmas = Sigmas.write(t, Sigma_t)
return tfp.distributions.MultivariateNormalFullCovariance(mus.stack(), Sigmas.stack())
def cov_to_corr(self, S):
"""
Transforms covariance matrix to a correlation matrix via matrix operations
Args:
S: Symmetric, positive semidefinite covariance matrix (tf.Tensor)
"""
D = tf.linalg.LinearOperatorDiag(1/(tf.linalg.diag_part(S)**0.5))
return D@S@D
def train_step(self, data):
"""
Custom training step to handle keras model.fit given that there is no input-output structure in our model
Args:
S: Symmetric, positive semidefinite covariance matrix (tf.Tensor)
"""
x,y = data
with tf.GradientTape() as tape:
loss = -tf.math.reduce_mean(self.get_log_probs(y))
trainable_vars = self.trainable_weights
gradients = tape.gradient(loss, trainable_vars)
self.optimizer.apply_gradients(zip(gradients, trainable_vars))
return {"Current loss": loss}
def sample_forecast(self, y, T_forecast = 30, n_samples=500):
"""
Create forecast samples to use for monte-carlo simulation of quantities of interest about the forecast (e.g. mean, var, corr, etc.)
WARNING: This is not optimized very much and can take some time to run, probably due to Python's slow loops - can likely be improved
Args:
y: numpy.array of training data, used to initialize the forecast values
T_forecast: number of periods to predict (integer)
n_samples: Number of samples to draw (integer)
"""
T = tf.shape(y)[0]
#create lists for looping; no gradients, thus no tf.TensorArrays needed
#can initialize directly
mus = []
Sigmas = []
us = [tf.zeros(shape=(self.n_dims,))]
sigmas = [self.sigma0]
Qs = []
#initialize remaining values for t=0
A0 = tf.transpose(self.L0)@self.L0
Qs.append(A0)
#convenience
sigma0 = self.sigma0
alpha0 = self.alpha0**2 #ensure positivity
alpha = self.alpha
beta = self.beta
A = self.A
B = self.B
#'warmup' to initialize latest lagged features
for t in range(T):
#tm1 = 't minus 1'
#suppress conditioning on past in notation
u_tm1 = us[-1]
sigma_tm1 = sigmas[-1]
sigma_t = (alpha0 + alpha*sigma_tm1**2 + beta*u_tm1**2)**0.5
u_tm1_standardized = u_tm1/sigma_tm1
Psi_tilde_tm1 = tf.reshape(u_tm1_standardized, (self.n_dims,1))@tf.reshape(u_tm1_standardized, (1,self.n_dims))
Q_tm1 = Qs[-1]
Q_t = A0 + A*(Q_tm1 - A0) + B*(Psi_tilde_tm1 - A0)
R_t = self.cov_to_corr(Q_t)
D_t = tf.linalg.LinearOperatorDiag(sigma_t)
Sigma_t = D_t@R_t@D_t
sigmas.append(sigma_t)
us.append(y[t,:]-self.MU) #we want to model the zero-mean disturbances
Qs.append(Q_t)
mus.append(self.MU)
Sigmas.append(Sigma_t)
#sample containers
y_samples = []
R_samples = []
sigma_samples = []
for n in range(n_samples):
mus_samp = []
Sigmas_samp = []
sigmas_samp = [sigmas[-1]]
us_samp = [us[-1]]
Qs_samp = [Qs[-1]]
#forecast containers
ys_samp = []
sig_samp = []
R_samp = []
for t in range(T_forecast):
u_tm1 = us_samp[-1]
sigma_tm1 = sigmas_samp[-1]
sigma_t = (alpha0 + alpha**2 + beta*u_tm1**2)**0.5
u_tm1_standardized = u_tm1/sigma_tm1
Psi_tilde_tm1 = tf.reshape(u_tm1_standardized, (self.n_dims,1))@tf.reshape(u_tm1_standardized, (1,self.n_dims))
Q_tm1 = Qs_samp[-1]
Q_t = A0 + A*(Q_tm1 - A0) + B*(Psi_tilde_tm1 - A0)
R_t = self.cov_to_corr(Q_t)
D_t = tf.linalg.LinearOperatorDiag(sigma_t)
Sigma_t = D_t@R_t@D_t
sigmas_samp.append(sigma_t)
Qs_samp.append(Q_t)
ynext = tfp.distributions.MultivariateNormalFullCovariance(self.MU, Sigma_t).sample()
ys_samp.append(tf.reshape(ynext,(1,1,-1)))
sig_samp.append(tf.reshape(sigma_t,(1,1,-1)))
R_samp.append(tf.reshape(R_t,(1,1,self.n_dims,self.n_dims)))
us_samp.append(ynext-self.MU)
y_samples.append(tf.concat(ys_samp,1))
R_samples.append(tf.concat(R_samp,1))
sigma_samples.append(tf.concat(sig_samp,1))
return tf.concat(y_samples,0).numpy(), tf.concat(R_samples,0).numpy(), tf.concat(sigma_samples,0).numpy()train = np.float32(returns)[:-90,:]
test = np.float32(returns)[-90:,:]model = MGARCH_DCC(train)
from scipy.stats import norm
out = model(train)
means = out.mean().numpy()
stds = out.stddev().numpy()
lowers = norm(means, stds).ppf(0.05)
uppers = norm(means, stds).ppf(0.95)
plt.figure(figsize = (16,6))
i = 0
plt.figure(figsize = (16,6))
plt.plot(train[:,i])
plt.fill_between(np.arange(len(train)),lowers[:,i],uppers[:,i],color="red",alpha=0.5)<Figure size 1152x432 with 0 Axes>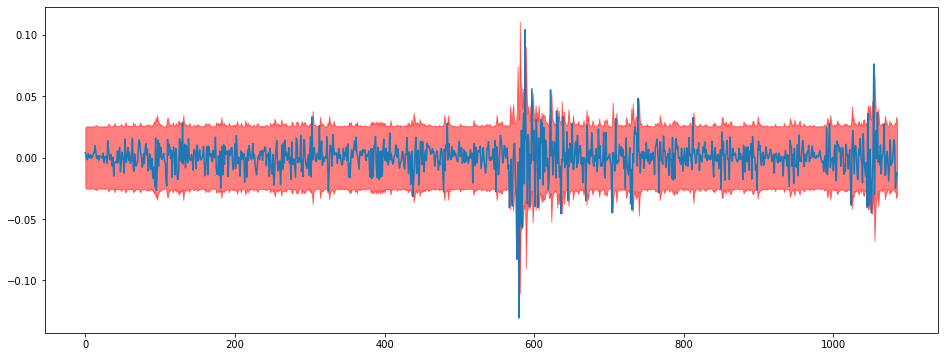
plt.figure(figsize = (16,6))
corr12 = [model.cov_to_corr(out.covariance()[i,:,:])[0,1].numpy() for i in range(len(train))]
plt.plot(corr12,c="red")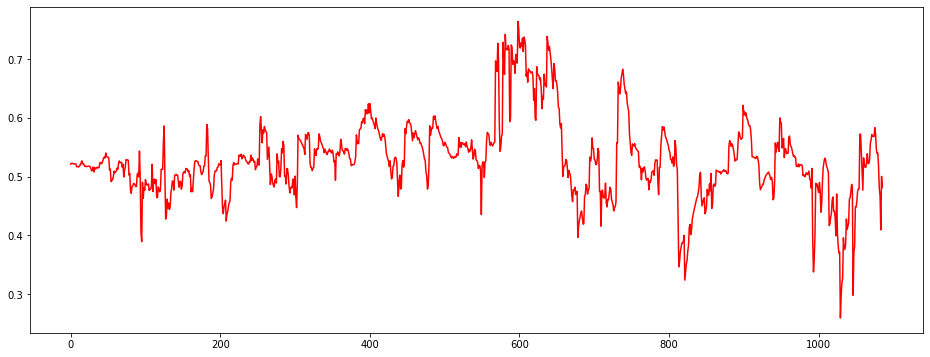
i = 1
plt.figure(figsize = (16,6))
plt.plot(train[:,i])
plt.fill_between(np.arange(len(train)),lowers[:,i],uppers[:,i],color="red",alpha=0.5)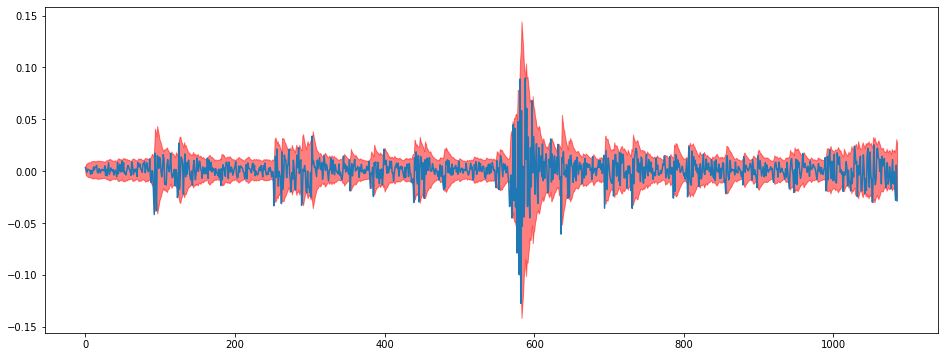
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-2))model.fit(train, train, batch_size=len(train), shuffle=False, epochs = 300, verbose=False)<keras.callbacks.History at 0x137bf2a40>out = model(train)
means = out.mean().numpy()
stds = out.stddev().numpy()
lowers = norm(means, stds).ppf(0.05)
uppers = norm(means, stds).ppf(0.95)i = 0
plt.figure(figsize = (16,6))
plt.plot(train[:,i])
plt.fill_between(np.arange(len(train)),lowers[:,i],uppers[:,i],color="red",alpha=0.5)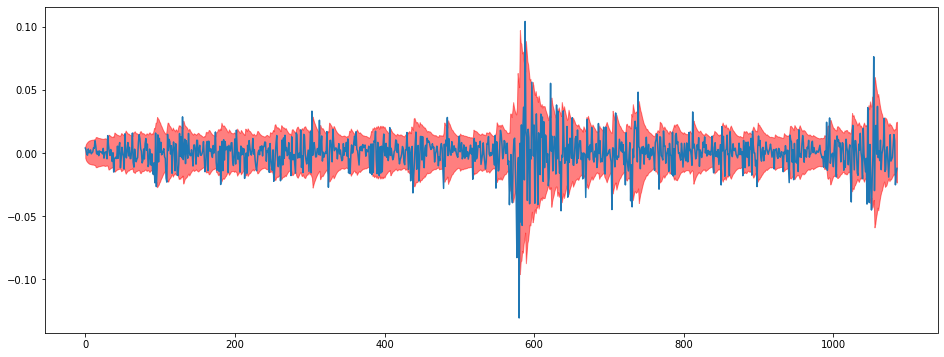
i = 1
plt.figure(figsize = (16,6))
plt.plot(train[:,i])
plt.fill_between(np.arange(len(train)),lowers[:,i],uppers[:,i],color="red",alpha=0.5)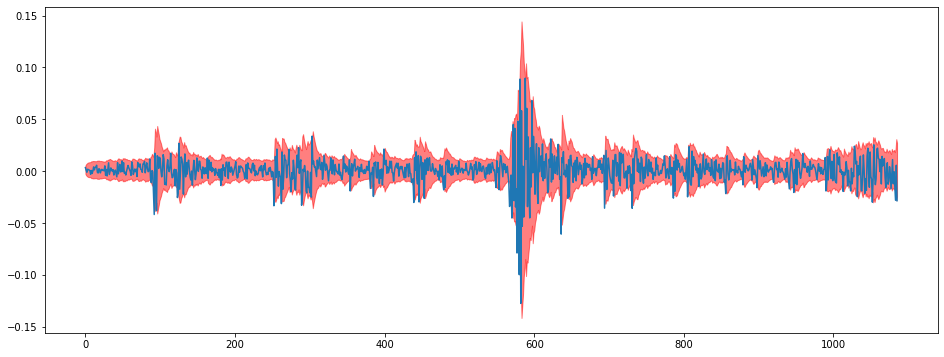
corr12 = [model.cov_to_corr(out.covariance()[i,:,:])[0,1].numpy() for i in range(len(train))]np.random.seed(123)
tf.random.set_seed(123)
fcast = model.sample_forecast(train,90,1000)corrs = fcast[1][:,:,0,1]
corr_means = np.mean(corrs,0)
corr_lowers = np.quantile(corrs,0.05,0)
corr_uppers = np.quantile(corrs,0.95,0)
conditional_dists = model(np.float32(returns.values))
conditional_correlations = [model.cov_to_corr(conditional_dists.covariance()[i,:,:])[0,1].numpy() for i in range(len(returns))]
idx_train = returns[:-90].index
idx_test = pd.date_range(returns[:-90].index[-1] + timedelta(days=1), returns[:-90].index[-1] + timedelta(days=90))
fig, axs = plt.subplots(2,1,figsize=(20,12), gridspec_kw={'height_ratios': [2, 1]})
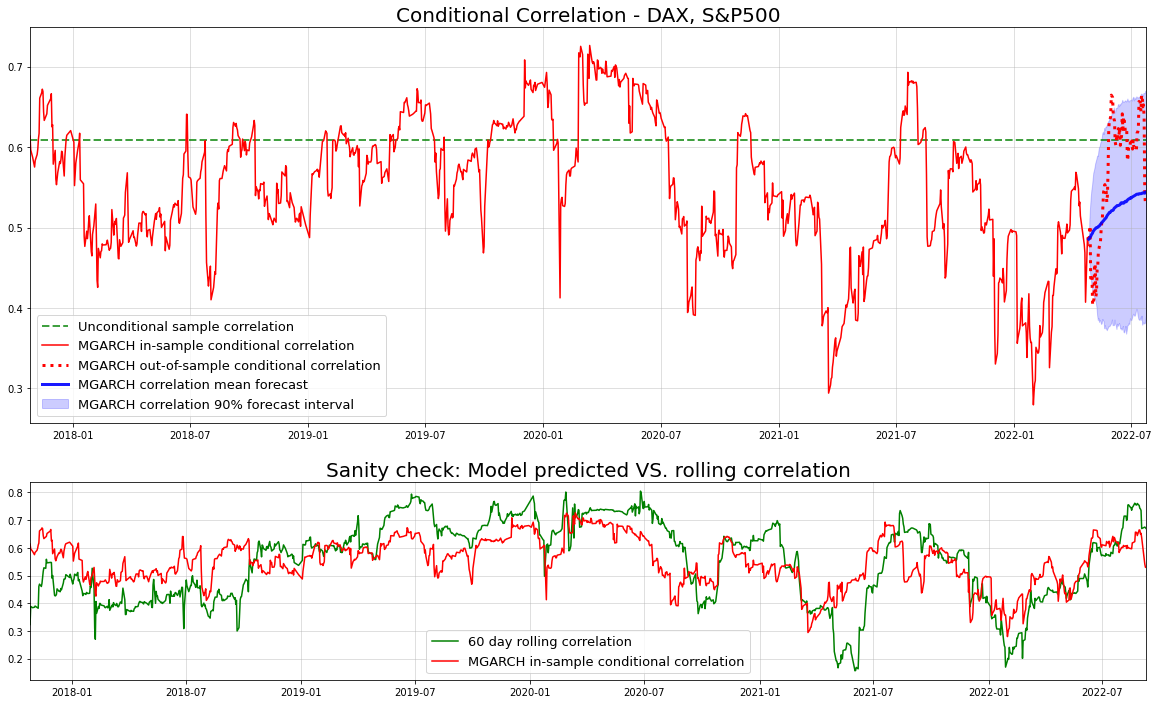
axs[0].set_title("Conditional Correlation - DAX, S&P500", size=20)
axs[0].axhline(np.corrcoef(returns.T)[0,1], c="green",alpha=0.75,ls="dashed",lw=2, label="Unconditional sample correlation")
axs[0].plot(idx_train[30:],conditional_correlations[30:-90],c="red", label="MGARCH in-sample conditional correlation")
axs[0].plot(idx_test,conditional_correlations[-90:],c="red",ls="dotted",lw=3, label="MGARCH out-of-sample conditional correlation")
axs[0].plot(idx_test, corr_means,color="blue",lw=3, alpha=0.9, label="MGARCH correlation mean forecast")
axs[0].fill_between(idx_test, corr_lowers, corr_uppers, color="blue", alpha=0.2, label="MGARCH correlation 90% forecast interval")
axs[0].grid(alpha=0.5)
axs[0].legend(prop = {"size":13})
axs[0].margins(x=0)
axs[1].set_title("Sanity check: Model predicted VS. rolling correlation",size=20)
axs[1].plot(returns.index[30:],gdaxi_sp500_rollcorr.values[30:],c="green", label="60 day rolling correlation")
axs[1].plot(returns.index[30:],conditional_correlations[30:],c="red", label="MGARCH in-sample conditional correlation")
axs[1].grid(alpha=0.5)
axs[1].legend(prop = {"size":13})
axs[1].margins(x=0)